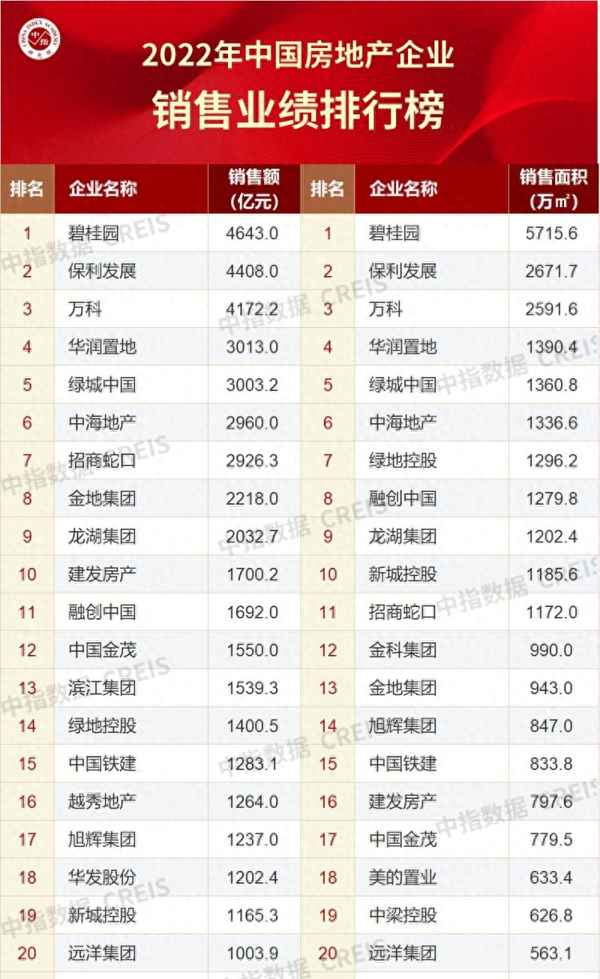
过阻尼的阻尼范围_过阻尼稳定吗

来源：中国人民教育出版社网，作者：何烈云。

简谐运动在不考虑摩擦和其他阻力等因素的影响时，振动过程中系统的机械能守恒，所以不管是单摆还是弹簧振子在振动过程中振幅始终保持不变，这种振动称为无阻尼振动。然而，实际的振动总要受到阻力的影响，由于要克服阻力做功，振动系统的机械能不断减少。同时振动系统与周围介质相互作用，振动向外传播形成波，随着波的传播，系统的机械能不断减少，因此振幅也逐渐减小。这种振幅逐渐减小的振动叫做阻尼振动，阻尼振动的图象如图1所示。

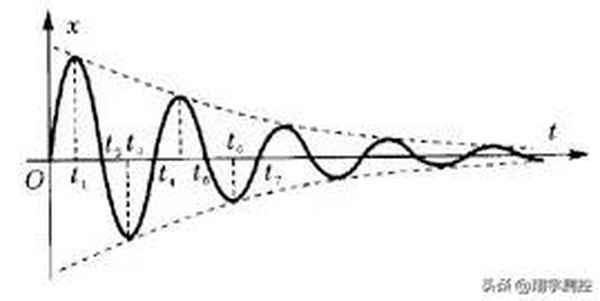
图1

在这两方面一般会存在这样的疑问：

• 一是，阻尼振动是否具有“周期性”；
• 二是，阻尼振动是否具有“等时性”（振子连续两次通过平衡位置的时间间隔相同）。

一、定性分析

要想知道阻尼振动是否具有“周期性”，首先要知道什么是机械振动的周期。定义是：物体完成一次全振动所需的时间，叫做振动的周期。在周期的定义中存在全振动这个概念，全振动是指做机械振动的物体从某个点出发，等到下次回到该点时的运动状态和开始振动时的运动状态完全相同，且所用时间最短。所以能重复原来的运动状态（位移、速度、加速度等）的机械振动才是全振动，非等幅的阻尼振动不是全振动，所以它是没有周期的。

关于阻尼振动是否具有“等时性”，有两种不同的说法：

• 第一种说法认为具有“等时性”，理由是阻尼振动的振幅虽然在不断减小，但可以看成是由很多个振幅不断减小的简谐运动的叠加，由于简谐运动具有等时性，它的周期与振幅无关，所以阻尼振动和简谐运动的相位是一致的，节奏也是相同的，所以具有“等时性”。
• 第二种说法认为不具有“等时性”，理由是物体做阻尼振动时，由于机械能的损失。振子前后两次通过同一点时，后一次的速度肯定比前一次的小。这样，从平衡位置到达最大位移处的平均速度总比返回时的平均速度大，所以回来就变慢了，对应的时间也就长了。按这种推理，阻尼振动的振动节奏会变得越来越慢，最后停止下来，周期变为无穷大，所以不具有“等时性”。

二、定量分析

弹簧振子在油中或较粘稠的液体中的缓慢运动是阻尼振动的典型例子，如图2所示，由流体力学可知，弹簧振子在油中或较粘稠的液体中运动时所受阻力的大小和速度的大小成正比，由牛顿第二定律，得

图2

式中，Υ 是阻尼系数。两边除以m，得

令

ω0为振动系统的固有圆频率；β 为阻尼系数，和振动系统的性质以及介质的性质有关。于是，方程可写为

这里我们讨论的是阻力很小的欠阻尼状态的阻尼振动，即β＜ω0，由上式可求出弹簧振子中质点的运动学方程为

式中，A 和a 为待定常数，由初始条件决定。此式中包含两个因子，Ae-βt 表示随时间衰减的振幅，cos(ω't＋a) 表示振动以ω' 为圆频率周期地变化，二因子相乘表示质点做运动范围不断缩小的往复运动。由于质点的运动状态不可能每经过一定时间便完全重复出现，因此阻尼振动不是周期运动。不过，cos(ω't＋a) 是周期变化的，它保证了质点每连续两次通过平衡位置并沿相同方向运动的时间间隔是相同的，可见“等时性”具有非常严格的条件。而且由于

大于弹簧振子系统的固有周期T=2π/ω0，可见阻尼振动的节奏变慢了。

三、结 论

比较由定性分析和定量分析得出的结论，阻尼振动不具有“周期性”的观点是相同的，但关于阻尼振动是否具有“等时性”的分析结果是不一样的。

只有通过定量分析的结论才是可靠的、正确的，仔细分析定性分析的两种说法中，推理都不严密并且是片面的，从而导致错误的结论。

• 定性分析中的第一种说法没有考虑到振子做阻尼振动时，由于阻力的影响回复力的大小不再和位移成正比，得出“阻尼振动和简谐运动相位是一致的，节奏也是相同的”的错误结论。
• 定性分析中的第二种说法只考虑了振子从平位置出发到达最大位移处，又从最大位移处返回到平衡位置，即在图1中的0～2 或2～4 这段时间的运动情况，没有把运动过程进行整体分析，从而忽视了在平均速度减小的同时，振子从平衡位置出发往复一次所经过的路程也变短了，导致得出错误的结论。

综上所述，阻尼振动不是周期性运动，但是质点连续两次通过平衡位置并沿相同方向运动所需的时间间隔是相同的。讨论阻尼振动时不能照搬简谐运动的规律，也不能做简单的定性分析，必要时还要做定量分析，否则就容易得出错误的结论。

参考文献：

漆安慎，杜弹英。力学。北京：高等教育出版社，1997．280～281

北京神州翔宇技术有限公司